Speicherplatz für PostgreSQL-B-Baum-Indexe richtig nutzen

Genau wie Tabellen speichert PostgreSQL auch die Daten von Indexen, die mit dem B-Tree-Verfahren erzeugt wurden, immer in 8 kByte großen Pages (solange die Pagegröße beim Kompilieren nicht geändert wurde). Die Anzahl an Pages, die Indexe und Tabellen für sich in Anspruch nehmen, sowie die Anzahl der abgelegten Tupel lässt sich einfach mithilfe der PostgreSQL-internen Tabelle »pg_class« herausfinden:

SELECT relname, reltuples, relpages
FROM pg_class
WHERE relname LIKE 't\_%';
 relname | reltuples | relpages
-----------+-----------+----------
 t_index | 10000 | 30
 t_tabelle | 10000 | 45

Zu sehen ist, dass der Index 30 und die Tabelle selbst 45 Pages in Anspruch nimmt. Wird die Anzahl der Pages mit 8 kByte multipliziert, so ergibt das den tatsächlichen Speicherverbrauch in kByte. Wenn alle Datensätze einer Tabelle gelöscht werden sollen, kommt häufig die Frage auf, was der Unterschied zwischen »DELETE« und »TRUNCATE« ist. Tatsächlich gibt es gleich zwei gravierende Unterschiede: Erstens gibt »DELETE« den Speicherplatz für eine Tabelle erst nach einem »VACUUM« an das System zurück – »TRUNCATE« dagegen sofort. Zweitens: TRUNCATE befreit auch den Index vom Ballast.

Ein kleines Experiment verdeutlicht das (Listing 1). Dort ist zu sehen, dass der Speicherplatz für die Tabelle erst nach »VACUUM ANALYZE« vollständig an das System zurückgegeben wurde. Der Index jedoch beansprucht danach immer noch 30 Pages für sich. Werden jetzt wieder 10000 Werte in die Tabelle eingespielt, legt die Datenbank für den Index 27 weitere Pages neu an, statt die vorhandenen 30 auszunutzen. Obwohl hier lediglich wieder genauso viele Zeilen eingefügt wie vorher gelöscht wurden, ist der Index fast doppelt so groß geworden. »DELETE« plus »VACUUM« reichen also nicht aus, um den Indexspeicher auf das kleinstmögliche Maß zu schrumpfen.

»TRUNCATE« gibt den Speicher sofort und unverzüglich zurück an das System (Listing 2). »TRUNCATE« hat nicht nur den Speicherplatz der Tabelle an das System zurückgegeben, sondern bis auf eine Page auch den Index vom Ballast befreit. Fügt man danach wie oben wieder 1000 Datensätze ein, ist der Index wieder so groß wie zu Anfang – und nicht verdoppelt, wie im ersten Beispiel.

Minimum ist eine Page

Aber warum hat Truncate beim Index eine Page stehen lassen? Die eine Page wird auch angelegt, wenn auf einer frischen, leeren Tabelle ein Index erzeugt wird: Ein Index nimmt immer mindestens 8 kByte in Anspruch. Diese erstePage enthält wichtige Metainformation. Jeder Index, egal ob leer oder nicht, braucht diese Page. Hier wird festgehalten, wo sich die Wurzel des Baumes befindet. Der eigentliche Indexbaum beginnt erst mit der zweiten Page. Wie sieht ein solcher B-Baum in PostgreSQL aus? Der B-Baum ist eine Datenstruktur, die schon 1972 von Rudolf Bayer, damals für Boeing tätig, und Edward M. McCreight entwickelt wurde. Die Entwickler haben bis heute nicht verraten, wofür das "B" steht. Die Interpretationen gehen von "Balanciert" über "Bayer" und "Boeing" bis hin zu "Barbara" (Bayers Frau). Für die Verwendung zum Speichern von Datenbank-Indexen warf der B-Baum-Algorithmus jedoch zunächst einige Fragen auf: Was ist mit zeitgleichen Zugriffen? Was ist mit Locking? Wie ist er MVCC-konform zu implementieren? Wie soll er sich beim Löschen verhalten? Über diese Themen haben unter anderem Phillip L. Lehman und S. Bing Yao sowie Vladimir Lanin und Dennis Shasha Abhandlungen geschrieben, die bei der PostgreSQL-Implementierung Berücksichtigung fanden. Bei der PostgreSQL-B-Baum-Implementierung handelt es sich um eine korrekte Implementierung des Lehman und Yao High-Concurrency B-Tree Management Algorithmus sowie einer vereinfachten Version der Lösch-Logik, die Lanin und Shasha beschrieben haben.

Einfaches Prinzip

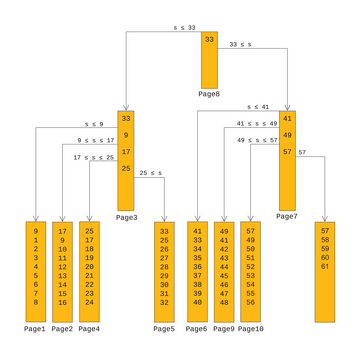
Das Prinzip des B-Baums ist einfach. Ganz unten befinden sich die Blätter (Leaves). Sie enthalten neben den indizierten Datenwerten (in Hex) den Link zu dem Tupel der zugehörigen Tabelle. Das obere Ende des Baumes markiert die Wurzel, in der ebenfalls ein Schlüsselwert hinterlegt ist. Es kann immer nur eine Wurzel geben. Die Ebenen zwischen Wurzel und Blättern enthalten innere Knoten, die den Baum in Unterbäume gliedern. Die inneren Knoten enthalten ebenfalls Schlüsselwerte, anhand derer der weitere Weg zu erkennen ist. Alle Schlüsselwerte, die kleiner als der Schlüssel der Wurzel sind, befinden sich auf der linken Seite des Baumes, alle anderen auf der rechten Seite. Abbildung 1 zeigt wie ein B-Baum aussehen könnte.

Abbildung 1: So könnte ein B-Baum-Index aussehen.

Wie viele Einträge auf eine Page passen, hängt von den indizierten Datensätzen ab. Bei einem Index über eine einzelne Integer-Spalte können durchaus mehrere Hundert auf eine Page passen. Der implementierte Algorithmus sieht jedoch vor, dass mindestens drei Einträge auf die Leave Pages passen müssen. PostgreSQL kann die Funktionalität nicht sicherstellen, wenn die Datensätze größer als 1/3 der Pagegröße sind. Um leere Pages in der Mitte zu vermeiden, muss eine linke Page immer mindestens zwei Datensätze enthalten. Wird der vorletzte Dateneintrag entfernt, sorgt das nächste »VACUUM« für eine Umsortierung.